欧美一区二区三区老妇人-欧美做爰猛烈大尺度电-99久久夜色精品国产亚洲a-亚洲福利视频一区二区

Java編程二項分布的遞歸和非遞歸實現代碼實例

本文研究的主要內容是Java編程二項分布的遞歸和非遞歸實現，具體如下。

大渡口網站制作公司哪家好，找創(chuàng)新互聯！從網頁設計、網站建設、微信開發(fā)、APP開發(fā)、成都響應式網站建設等網站項目制作，到程序開發(fā)，運營維護。創(chuàng)新互聯從2013年開始到現在10年的時間，我們擁有了豐富的建站經驗和運維經驗，來保證我們的工作的順利進行。專注于網站建設就選創(chuàng)新互聯。

問題來源：

算法第四版 第1.1節(jié) 習題27：return (1.0 - p) * binomial(N - 1, k, p) + p * binomial(N - 1, k - 1, p);
計算遞歸調用次數，這里的遞歸式是怎么來的？

二項分布:

定義：n個獨立的是/非試驗中成功次數k的離散概率分布，每次實驗成功的概率為p，記作B(n,p,k)。

概率公式：P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k)

其中C(n, k) = (n-k) !/(k! * (n-k)!)，記作ξ~B(n,p)，期望：Eξ=np，方差:Dξ=npq，其中q=1-p。

概率統計里有一條遞歸公式：

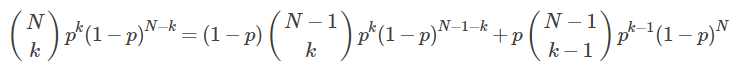
Java編程二項分布的遞歸和非遞歸實現代碼實例

這個便是題目中遞歸式的來源。

該遞推公式來自:C(n,k)=C(n-1,k)+C(n-1,k-1)。實際場景是從n個人選k個，有多少種組合？將著n個人按1~n的順序排好，假設第k個人沒被選中，則需要從剩下的n-1個人中選k個；第k個選中了，則需要從剩下的n-1個人中選k-1個。

書中二項分布的遞歸實現：

public static double binomial(int N, int k, double p) { 
    COUNT++; //記錄遞歸調用次數 
    if (N == 0 && k == 0) { 
      return 1.0; 
    } 
    if (N < 0 || k < 0) { 
      return 0.0; 
    } 
    return (1.0 - p) * binomial(N - 1, k, p) + p * binomial(N - 1, k - 1, p); 
  }

實驗結果：

n   k   p   調用次數
10  5  0.25  2467
20  10  0.25  2435538
30  15  0.25  2440764535

由結果可以看出來這個遞歸方法需要調用的次數呈幾何災難，n到50就算不下去了。

改進的二項分布遞歸實現：

private static long COUNT = 0; 
  private static double[][] M; 
   
  private static double binomial(int N, int k, double p) { 
    COUNT++; 
    if (N == 0 && k == 0) { 
      return 1.0; 
    } 
    if (N < 0 || k < 0) { 
      return 0.0; 
    } 
    if (M[N][k] == -1) { //將計算結果存起來，已經計算過的直接拿過來用，無需再遞歸計算 
      M[N][k] = (1.0 - p) * binomial(N - 1, k, p) + p * binomial(N - 1, k - 1, p); 
    } 
    return M[N][k]; 
  } 
 
  public static double Binomial(int N, int k, double p) { 
    M = new double[N + 1][k + 1]; 
    for (int i = 0; i <= N; i++) { 
      for (int j = 0; j <= k; j++) { 
        M[i][j] = -1; 
      } 
    } 
    return binomial(N, k, p); 
  }

實驗結果：

n    k   p   調用次數
10    5  0.25  101
20   10  0.25  452
30   15  0.25  1203
50   25  0.25  3204
100  50  0.25  5205

由實驗結果可以看出調用次數大幅減小，算法可以使用。

二項分布的非遞歸實現：

事實上，不利用遞歸，直接計算組合數和階乘，反而速度更快。

//計算組合數 
public static double combination(double N, double k) 
{ 
  double min = k; 
  double max = N-k; 
  double t = 0; 
 
  double NN=1; 
  double kk=1; 
   
  if(min>max){ 
    t=min; 
    min = max; 
    max=t; 
  } 
   
  while(N>max){//分母中較大的那部分階乘約分不用計算 
    NN=NN*N; 
    N--; 
  } 
   
  while(min>0){//計算較小那部分的階乘 
    kk=kk*min; 
    min--; 
  } 
   
  return NN/kk; 
} 
 
//計算二項分布值 
public static double binomial(int N,int k,double p) 
{ 
  double a=1; 
  double b=1; 
   
  double c =combination(N,k); 
   
  while((N-k)>0){ //計算(1-p)的(N-k)次方     
    a=a*(1-p); 
    N--; 
  } 
   
  while(k>0){ //計算p的k次方   
    b=b*p; 
    k--; 
  } 
   
  return c*a*b; 
}

實驗結果：

n   k  p      二項分布值
10,  5, 0.25  0.058399200439453125
20, 10, 0.25 0.009922275279677706
50, 25, 0.25  8.44919466990397E-5

與前面的算法比對，計算結果是正確的，而且運行速度是非常之快的。

總結

以上就是本文關于Java編程二項分布的遞歸和非遞歸實現代碼實例的全部內容，希望對大家有所幫助。感興趣的朋友可以繼續(xù)參閱本站其他相關專題，如有不足之處，歡迎留言指出。感謝朋友們對本站的支持！

當前題目：Java編程二項分布的遞歸和非遞歸實現代碼實例
URL地址：http://www.chinadenli.net/article14/iiejge.html

成都網站建設公司_創(chuàng)新互聯，為您提供外貿網站建設、定制開發(fā)、全網營銷推廣、網站策劃、云服務器、外貿建站

廣告

聲明：本網站發(fā)布的內容（圖片、視頻和文字）以用戶投稿、用戶轉載內容為主，如果涉及侵權請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網站立場，如需處理請聯系客服。電話：028-86922220；郵箱：631063699@qq.com。內容未經允許不得轉載，或轉載時需注明來源： 創(chuàng)新互聯

成都網站建設公司