小編這次要給大家分享的是C++如何實(shí)現(xiàn)求等差素?cái)?shù)列，文章內(nèi)容豐富，感興趣的小伙伴可以來(lái)了解一下，希望大家閱讀完這篇文章之后能夠有所收獲。

成都創(chuàng)新互聯(lián)是一家網(wǎng)站設(shè)計(jì)公司，集創(chuàng)意、互聯(lián)網(wǎng)應(yīng)用、軟件技術(shù)為一體的創(chuàng)意網(wǎng)站建設(shè)服務(wù)商，主營(yíng)產(chǎn)品：成都響應(yīng)式網(wǎng)站建設(shè)公司、品牌網(wǎng)站制作、成都營(yíng)銷網(wǎng)站建設(shè)。我們專注企業(yè)品牌在網(wǎng)站中的整體樹立，網(wǎng)絡(luò)互動(dòng)的體驗(yàn)，以及在手機(jī)等移動(dòng)端的優(yōu)質(zhì)呈現(xiàn)。成都網(wǎng)站設(shè)計(jì)、成都網(wǎng)站建設(shè)、外貿(mào)網(wǎng)站建設(shè)、移動(dòng)互聯(lián)產(chǎn)品、網(wǎng)絡(luò)運(yùn)營(yíng)、VI設(shè)計(jì)、云產(chǎn)品.運(yùn)維為核心業(yè)務(wù)。為用戶提供一站式解決方案，我們深知市場(chǎng)的競(jìng)爭(zhēng)激烈，認(rèn)真對(duì)待每位客戶，為客戶提供賞析悅目的作品，網(wǎng)站的價(jià)值服務(wù)。

題目

標(biāo)題：等差素?cái)?shù)列

2,3,5,7,11,13,....是素?cái)?shù)序列。
類似：7,37,67,97,127,157 這樣完全由素?cái)?shù)組成的等差數(shù)列，叫等差素?cái)?shù)數(shù)列。
上邊的數(shù)列公差為30，長(zhǎng)度為6。

2004年，格林與華人陶哲軒合作證明了：存在任意長(zhǎng)度的素?cái)?shù)等差數(shù)列。
這是數(shù)論領(lǐng)域一項(xiàng)驚人的成果！

有這一理論為基礎(chǔ)，請(qǐng)你借助手中的計(jì)算機(jī)，滿懷信心地搜索：

長(zhǎng)度為10的等差素?cái)?shù)列，其公差最小值是多少？

注意：需要提交的是一個(gè)整數(shù)，不要填寫任何多余的內(nèi)容和說(shuō)明文字。

題解

絮絮叨叨（罵罵咧咧

一開始看到這道題還是有點(diǎn)懵的，畢竟我個(gè)數(shù)學(xué)小白，對(duì)素?cái)?shù)什么的最發(fā)怵了。

然后找了好多大佬的題解都沒看明白，甚至有一個(gè)大佬的代碼看的我暈頭轉(zhuǎn)向~

然后終于被我找到一份能看懂并且覺得非常正確的代碼，思路如下：

思路

兩層循環(huán)，一層循環(huán)用于循環(huán)公差，一層循環(huán)用于循環(huán)起始素?cái)?shù)。

需要注意的是，內(nèi)層循環(huán)起始素?cái)?shù)的時(shí)候，不能無(wú)邊界循環(huán)下去，要設(shè)置一個(gè)上限，否則外層循環(huán)永遠(yuǎn)無(wú)法走到下一個(gè)公差（自己寫的時(shí)候自以為是犯的錯(cuò)

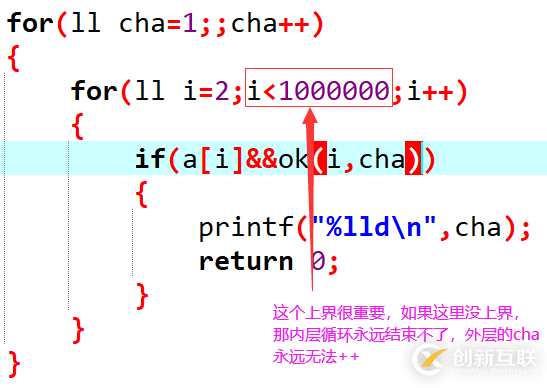
內(nèi)層循環(huán)走的時(shí)候，只需要判斷：
①這個(gè)數(shù)是不是素?cái)?shù)（作為起始素?cái)?shù)最基本的條件）
②判斷從這個(gè)素?cái)?shù)開始，以cha為公差能否存在連續(xù)10個(gè)等差的素?cái)?shù)。【用ok函數(shù)來(lái)判斷的】

如果以上兩個(gè)條件都滿足，則這就是我們要找的長(zhǎng)度為10的等差素?cái)?shù)列，其公差的最小值

因?yàn)槲覀兪菑男〉酱笳业模俏覀冋业降臐M足條件的第一個(gè)就是答案~

#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll maxn=1e6+50;
ll a[maxn];
bool ok(ll n,ll cha)
{
	for(ll i=0;i<10;i++)
	{
		if(!a[n+i*cha])return 0;
	}
	return 1;
}

int main()
{
	a[1]=0;
	a[2]=1;
	a[3]=1;
	for(ll i=4;i<=1000000;i++)
	{
		bool flag=0;
		for(ll j=2;j*j<=i;j++)
		{
			if(i%j==0)
			{
				flag=1;
				break;
			}
		}
		if(flag)a[i]=0;
		else a[i]=1;
	}
	
	for(ll cha=1;;cha++)
	{
		for(ll i=2;i<1000000;i++)
		{
			if(a[i]&&ok(i,cha))
			{
				printf("%lld\n",cha);
				return 0;
			}
		}
	}
}

新聞標(biāo)題：C++如何實(shí)現(xiàn)求等差素?cái)?shù)列-創(chuàng)新互聯(lián)
文章出自：http://www.chinadenli.net/article48/dpdjep.html

成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián)，為您提供微信公眾號(hào)、網(wǎng)站建設(shè)、營(yíng)銷型網(wǎng)站建設(shè)、品牌網(wǎng)站建設(shè)、域名注冊(cè)、網(wǎng)頁(yè)設(shè)計(jì)公司

廣告

聲明：本網(wǎng)站發(fā)布的內(nèi)容（圖片、視頻和文字）以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主，如果涉及侵權(quán)請(qǐng)盡快告知，我們將會(huì)在第一時(shí)間刪除。文章觀點(diǎn)不代表本網(wǎng)站立場(chǎng)，如需處理請(qǐng)聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載，或轉(zhuǎn)載時(shí)需注明來(lái)源： 創(chuàng)新互聯(lián)