本篇文章給大家分享的是有關(guān)怎么在Java項目中實現(xiàn)一個矩陣乘法，小編覺得挺實用的，因此分享給大家學(xué)習(xí)，希望大家閱讀完這篇文章后可以有所收獲，話不多說，跟著小編一起來看看吧。

創(chuàng)新互聯(lián)是少有的網(wǎng)站建設(shè)、做網(wǎng)站、營銷型企業(yè)網(wǎng)站、微信小程序、手機APP,開發(fā)、制作、設(shè)計、買鏈接、推廣優(yōu)化一站式服務(wù)網(wǎng)絡(luò)公司,于2013年創(chuàng)立,堅持透明化,價格低,無套路經(jīng)營理念。讓網(wǎng)頁驚喜每一位訪客多年來深受用戶好評

矩陣乘法過程展示

C[1][1] = A[1][0] * B[0][1] + A[1][1] * B[1][1] + A[1][2] * B[2][1] + A[1][3] * B[3][1] + A[1][4] * B[4][1]

??而用Java實現(xiàn)該過程的傳統(tǒng)方法就是按照該規(guī)則實現(xiàn)一個三重循環(huán)，把各項乘積累加：

public int[][] multiply(int[][] mat1, int[][] mat2){
	int m = mat1.length, n = mat2[0].length;
	int[][] mat = new int[m][n];
	for(int i = 0; i < m; i++){
		for(int j = 0; j < n; j++){
			for(int k = 0; k < mat1[0].length; k++){
				mat[i][j] += mat1[i][k] * mat2[k][j];
			}
		}
	}
	return mat;
}

??可以看出該方法的時間復(fù)雜度為O(n3)，當(dāng)矩陣維數(shù)比較大的時候程序就很容易超時。

優(yōu)化方法（Strassen算法）

??Strassen算法是由Volker Strassen在1966年提出的第一個時間復(fù)雜度低于O(n³)的矩陣乘法算法，其主要思想是通過分治來實現(xiàn)矩陣乘法的快速運算，計算過程如圖所示：

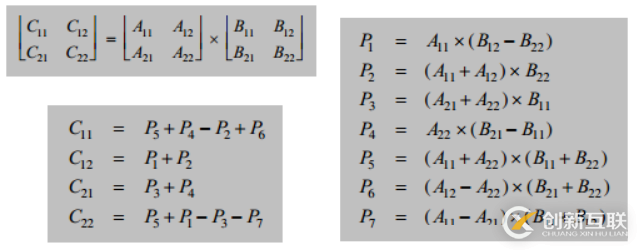
將一次矩陣乘法拆分成多個乘法與加法的結(jié)合

??為什么這個方法會更快呢，我們知道，按照傳統(tǒng)的矩陣乘法：

C11 = A11 * B11 + A12 * B21
C12 = A11 * B12 + A12 * B22
C21 = A21 * B11 + A22 * B21
C22 = A21 * B12 + A22 * B22

??我們需要8次矩陣乘法和4次矩陣加法，正是這8次乘法最耗時；而Strassen方法只需要7次矩陣乘法，盡管代價是矩陣加法次數(shù)變?yōu)?8次，但是基于數(shù)量級考慮，18次加法仍然快于1次乘法。

??當(dāng)然，Strassen算法的代碼實現(xiàn)也比傳統(tǒng)算法復(fù)雜許多，這里附上另一個大神寫的java實現(xiàn)（原文鏈接：https://www.jb51.net/article/205375.htm）：

public class Matrix {
	private final Matrix[] _matrixArray;
	private final int n;
	private int element;
	public Matrix(int n) {
		this.n = n;
		if (n != 1) {
			this._matrixArray = new Matrix[4];
			for (int i = 0; i < 4; i++) {
				this._matrixArray[i] = new Matrix(n / 2);
			}
		} else {
			this._matrixArray = null; 
		}
	}
	private Matrix(int n, boolean needInit) {
		this.n = n;
		if (n != 1) {
			this._matrixArray = new Matrix[4];
		} else {
			this._matrixArray = null; 
		}
	}
	public void set(int i, int j, int a) {
		if (n == 1) {
			element = a;
		} else {
			int size = n / 2;
			this._matrixArray[(i / size) * 2 + (j / size)].set(i % size, j % size, a);
		}
	}
	public Matrix multi(Matrix m) {
		Matrix result = null;
		if (n == 1) {
			result = new Matrix(1);
			result.set(0, 0, (element * m.element));
		} else {
			result = new Matrix(n, false);
			result._matrixArray[0] = P5(m).add(P4(m)).minus(P2(m)).add(P6(m));
			result._matrixArray[1] = P1(m).add(P2(m));
			result._matrixArray[2] = P3(m).add(P4(m));
			result._matrixArray[3] = P5(m).add(P1(m)).minus(P3(m)).minus(P7(m));
		}
		return result;
	}
	public Matrix add(Matrix m) {
		Matrix result = null;
		if (n == 1) {
			result = new Matrix(1);
			result.set(0, 0, (element + m.element));
		} else {
			result = new Matrix(n, false);
			result._matrixArray[0] = this._matrixArray[0].add(m._matrixArray[0]);
			result._matrixArray[1] = this._matrixArray[1].add(m._matrixArray[1]);
			result._matrixArray[2] = this._matrixArray[2].add(m._matrixArray[2]);
			result._matrixArray[3] = this._matrixArray[3].add(m._matrixArray[3]);;
		}
		return result;
	}
	public Matrix minus(Matrix m) {
		Matrix result = null;
		if (n == 1) {
			result = new Matrix(1);
			result.set(0, 0, (element - m.element));
		} else {
			result = new Matrix(n, false);
			result._matrixArray[0] = this._matrixArray[0].minus(m._matrixArray[0]);
			result._matrixArray[1] = this._matrixArray[1].minus(m._matrixArray[1]);
			result._matrixArray[2] = this._matrixArray[2].minus(m._matrixArray[2]);
			result._matrixArray[3] = this._matrixArray[3].minus(m._matrixArray[3]);;
		}
		return result;
	}
	protected Matrix P1(Matrix m) {
		return _matrixArray[0].multi(m._matrixArray[1]).minus(_matrixArray[0].multi(m._matrixArray[3]));
	}
	protected Matrix P2(Matrix m) {
		return _matrixArray[0].multi(m._matrixArray[3]).add(_matrixArray[1].multi(m._matrixArray[3]));
	}
	protected Matrix P3(Matrix m) {
		return _matrixArray[2].multi(m._matrixArray[0]).add(_matrixArray[3].multi(m._matrixArray[0]));
	}
	protected Matrix P4(Matrix m) {
		return _matrixArray[3].multi(m._matrixArray[2]).minus(_matrixArray[3].multi(m._matrixArray[0]));
	}
	protected Matrix P5(Matrix m) {
		return (_matrixArray[0].add(_matrixArray[3])).multi(m._matrixArray[0].add(m._matrixArray[3]));
	}
	protected Matrix P6(Matrix m) {
		return (_matrixArray[1].minus(_matrixArray[3])).multi(m._matrixArray[2].add(m._matrixArray[3]));
	}
	protected Matrix P7(Matrix m) {
		return (_matrixArray[0].minus(_matrixArray[2])).multi(m._matrixArray[0].add(m._matrixArray[1]));
	}
	public int get(int i, int j) {
		if (n == 1) {
			return element;
		} else {
			int size = n / 2;
			return this._matrixArray[(i / size) * 2 + (j / size)].get(i % size, j % size);
		}
	}
	public void display() {
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				System.out.print(get(i, j));
				System.out.print(" ");
			}
			System.out.println();
		}
	}
	
	public static void main(String[] args) {
		Matrix m = new Matrix(2);
		Matrix n = new Matrix(2);
		m.set(0, 0, 1);
		m.set(0, 1, 3);
		m.set(1, 0, 5);
		m.set(1, 1, 7);
		n.set(0, 0, 8);
		n.set(0, 1, 4);
		n.set(1, 0, 6);
		n.set(1, 1, 2);
		Matrix res = m.multi(n);
		res.display();
	}
}

以上就是怎么在Java項目中實現(xiàn)一個矩陣乘法，小編相信有部分知識點可能是我們?nèi)粘９ぷ鲿姷交蛴玫降摹ＯＭ隳芡ㄟ^這篇文章學(xué)到更多知識。更多詳情敬請關(guān)注創(chuàng)新互聯(lián)行業(yè)資訊頻道。

當(dāng)前名稱：怎么在Java項目中實現(xiàn)一個矩陣乘法-創(chuàng)新互聯(lián)
瀏覽地址：http://www.chinadenli.net/article38/djdjpp.html

成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián)，為您提供外貿(mào)建站、網(wǎng)站內(nèi)鏈、關(guān)鍵詞優(yōu)化、品牌網(wǎng)站制作、網(wǎng)站改版、企業(yè)建站

廣告

聲明：本網(wǎng)站發(fā)布的內(nèi)容（圖片、視頻和文字）以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主，如果涉及侵權(quán)請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網(wǎng)站立場，如需處理請聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載，或轉(zhuǎn)載時需注明來源： 創(chuàng)新互聯(lián)