今天我們來(lái)看下算法復(fù)雜度和效率的問(wèn)題，在判斷一個(gè)算法的效率時(shí)，操作數(shù)量中的常數(shù)項(xiàng)和其他次要項(xiàng)常常是可以忽略的，只需要關(guān)注最高階項(xiàng)就能得出結(jié)論。那么我們?nèi)绾斡梅?hào)定性的判斷算法的效率呢？算法的復(fù)雜度分為兩部分：1、時(shí)間復(fù)雜度，即算法運(yùn)行后對(duì)時(shí)間需求量的定性描述；2、空間復(fù)雜度，即算法運(yùn)行后對(duì)空間需求量的定性描述。

創(chuàng)新互聯(lián)公司專注于集美企業(yè)網(wǎng)站建設(shè),成都響應(yīng)式網(wǎng)站建設(shè),成都商城網(wǎng)站開(kāi)發(fā)。集美網(wǎng)站建設(shè)公司,為集美等地區(qū)提供建站服務(wù)。全流程按需網(wǎng)站建設(shè)，專業(yè)設(shè)計(jì)，全程項(xiàng)目跟蹤，創(chuàng)新互聯(lián)公司專業(yè)和態(tài)度為您提供的服務(wù)

數(shù)據(jù)結(jié)構(gòu)重點(diǎn)關(guān)注的是算法的效率問(wèn)題，因此，我們后面會(huì)集中于討論算法的時(shí)間復(fù)雜度；但其使用的方法完全可以用于空間復(fù)雜度的判斷！我們經(jīng)常在進(jìn)行算法的時(shí)間復(fù)雜度用大O表示法來(lái)進(jìn)行分析。下來(lái)對(duì)此種方法進(jìn)行說(shuō)明，算法效率嚴(yán)重依賴于操作（Operation）數(shù)量；操作數(shù)量的估算可以作為時(shí)間復(fù)雜度的估算；在判斷時(shí)首先關(guān)注操作數(shù)量的最高次項(xiàng)。如下：

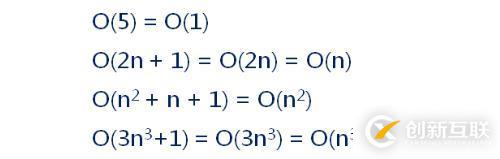
下來(lái)我們來(lái)分析下常見(jiàn)的時(shí)間復(fù)雜度：

1、線性階時(shí)間復(fù)雜度：O(n)。如下：

2、對(duì)數(shù)階時(shí)間復(fù)雜度：O(logn)。如下

3、平方階時(shí)間復(fù)雜度：O(n2)。如下：

下來(lái)我們來(lái)看看常見(jiàn)的時(shí)間復(fù)雜度，如下圖所示

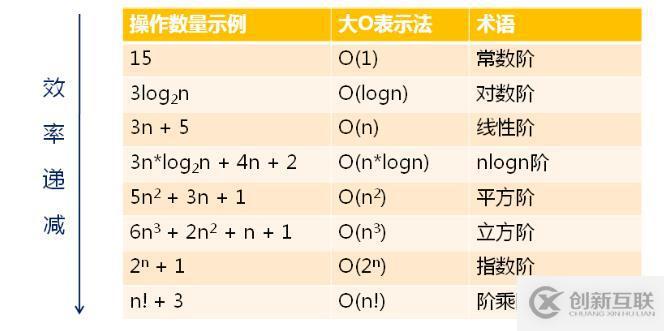
常見(jiàn)的時(shí)間復(fù)雜度的比較，如下

下面我們通過(guò)實(shí)例來(lái)進(jìn)行分析下，下面的函數(shù)程序復(fù)雜度是怎樣的

int?find(int?a[],?int?n,?int?v)
{
????int?ret?=?-1;
????
????for(int?i=0;?i<=n;?i++)
????{
????????if(?a[i]?==?v?)
????????{
????????????ret?=?i;
????????????break;
????????}
????}
????
????return?ret;
}

我們?nèi)绻x的數(shù)組 a[5] = {1, 2, 3, 4, 5}； 如果是 int min = find(a, 5, 1)； 這種則是最好情況了，僅需執(zhí)行 1 次循環(huán)，此時(shí)便是 O(1)；如果是 int max = find(a, 5, 5)；此時(shí)便是最壞的情況了，需要全部執(zhí)行，此時(shí)便是 O(n)。那么此時(shí)算法的最好與最壞情況便體現(xiàn)出來(lái)了，當(dāng)算法在最乖情況下仍然能滿足需求時(shí)，可以推斷，算法的最好情況和平均情況都滿足需求。在以后沒(méi)有進(jìn)行特殊說(shuō)明時(shí)，所分析算法的時(shí)間復(fù)雜度都是指最壞時(shí)間復(fù)雜度。

算法的空間復(fù)雜度（Space Complexity），其定義為 S(n) = S(f(n))。其中 n 為算法的問(wèn)題規(guī)模，f(n) 為空間使用函數(shù)，與 n 相關(guān)。推倒時(shí)間復(fù)雜度的方法同樣適用于空間復(fù)雜度，例如，當(dāng)算法所需要的空間是常數(shù)時(shí)，其空間復(fù)雜度為 S(1)。我么來(lái)看看下面這個(gè)程序的空間復(fù)雜度為多少

long?sum1(int?n)
{
????long?ret?=?0;
????int*?array?=?new?int[n];
????
????for(int?i=0;?i<n;?i++)
????{
????????array[i]?=?i?+?1;
????}
????
????for(iunt?i=0;?i<n;?i++)
????{
????????ret?+=?array[i];
????}
????
????delete[]?array;
????
????return?ret;
}

我們看到第一行為 1，第三行的 ret 定義也為 1，指針數(shù)組 array 的定義其空間復(fù)雜度為 n，下面兩個(gè)進(jìn)行 for 循環(huán)的空間復(fù)雜度分別為 1。因此整個(gè)程序所需的單位內(nèi)存為： n + 4；即空間復(fù)雜度：S(n+4) = S(n)。那么時(shí)間跟空間之間是否存在某種聯(lián)系呢？在多數(shù)情況下，算法的時(shí)間復(fù)雜度更令人關(guān)注，因?yàn)楝F(xiàn)在的內(nèi)存都很大。如果有必要的話，可以通過(guò)增加額外空間降低時(shí)間復(fù)雜度；同理，也可以增加算法的耗時(shí)降低空間復(fù)雜度。下來(lái)我們來(lái)看個(gè)空間換時(shí)間的示例代碼，代碼的背景是在 1-1000 中的某些數(shù)字搜組成的數(shù)組中，設(shè)計(jì)一個(gè)算法類找出出現(xiàn)次數(shù)最多的數(shù)字。

#include?<iostream>

using?namespace?std;

void?sreach(int?a[],?int?len)
{
????int?pi[1000]?=?{0};
????int?max?=?0;
????
????for(int?i=0;?i<len;?i++)
????{
????????pi[a[i]?-1]++;
????}
????
????for(int?i=0;?i<1000;?i++)
????{
????????if(?max?<?pi[i]?)
????????{
????????????max?=?pi[i];
????????}
????}
????
????for(int?i=0;?i<1000;?i++)
????{
????????if(?max?==?pi[i]?)
????????{
????????????cout?<<?i?+?1?<<?endl;
????????}
????}
}

int?main(int?argc,?char*?argv[])
{
????int?a[]?=?{1,?1,?3,?4,?5,?6,?6,?6,?3,?3};
????
????sreach(a,?sizeof(a)/sizeof(*a));
????
????return?0;
}

我們來(lái)看看打印結(jié)果

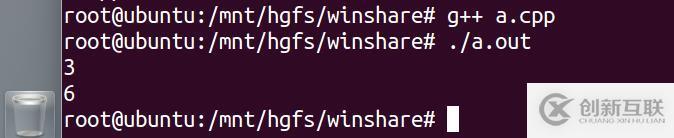
我們看到打印了 3 和 6，因?yàn)榇髷?shù) 6 和 3 都出現(xiàn)了 3 次。那么此次我們的程序?qū)崿F(xiàn)中函數(shù)的時(shí)間復(fù)雜度為 O(n)。那么問(wèn)題來(lái)了，當(dāng)兩個(gè)算法的大 O 表示法相同時(shí)，是否意味著兩個(gè)算法的效率完全相同呢？肯定是不相同的！通過(guò)今天對(duì)算法的時(shí)間復(fù)雜度和效率的學(xué)習(xí)，總結(jié)如下：1、時(shí)間復(fù)雜度是算法運(yùn)行時(shí)對(duì)于時(shí)間的需求量；2、大 O 表示法用于描述算法的時(shí)間復(fù)雜度，它只關(guān)注操作數(shù)量的最高次項(xiàng)；3、常見(jiàn)的時(shí)間復(fù)雜度為：線性階，平方階和對(duì)數(shù)階；4、一般而言，在工程中使用的算法其復(fù)雜度都不超過(guò) O(n3)；5、算法分析與設(shè)計(jì)時(shí)，重點(diǎn)考慮最壞情況下的時(shí)間復(fù)雜度，大 O 表示法用于適用于算法的空間復(fù)雜度；6、空間換時(shí)間是工程開(kāi)發(fā)中常用的策略。

標(biāo)題名稱：算法時(shí)間復(fù)雜度及效率（二）-創(chuàng)新互聯(lián)
本文路徑：http://www.chinadenli.net/article26/dhescg.html

成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián)，為您提供網(wǎng)站排名、全網(wǎng)營(yíng)銷推廣、做網(wǎng)站、品牌網(wǎng)站設(shè)計(jì)、響應(yīng)式網(wǎng)站、電子商務(wù)

廣告

聲明：本網(wǎng)站發(fā)布的內(nèi)容（圖片、視頻和文字）以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主，如果涉及侵權(quán)請(qǐng)盡快告知，我們將會(huì)在第一時(shí)間刪除。文章觀點(diǎn)不代表本網(wǎng)站立場(chǎng)，如需處理請(qǐng)聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載，或轉(zhuǎn)載時(shí)需注明來(lái)源： 創(chuàng)新互聯(lián)