這篇文章主要介紹了Sklearn廣義線性模型實例分析的相關(guān)知識，內(nèi)容詳細易懂，操作簡單快捷，具有一定借鑒價值，相信大家閱讀完這篇Sklearn廣義線性模型實例分析文章都會有所收獲，下面我們一起來看看吧。

成都創(chuàng)新互聯(lián)主要為客戶提供服務(wù)項目涵蓋了網(wǎng)頁視覺設(shè)計、VI標(biāo)志設(shè)計、全網(wǎng)整合營銷推廣、網(wǎng)站程序開發(fā)、HTML5響應(yīng)式成都網(wǎng)站建設(shè)、手機網(wǎng)站制作、微商城、網(wǎng)站托管及成都網(wǎng)站維護公司、WEB系統(tǒng)開發(fā)、域名注冊、國內(nèi)外服務(wù)器租用、視頻、平面設(shè)計、SEO優(yōu)化排名。設(shè)計、前端、后端三個建站步驟的完善服務(wù)體系。一人跟蹤測試的建站服務(wù)標(biāo)準(zhǔn)。已經(jīng)為人造霧行業(yè)客戶提供了網(wǎng)站設(shè)計服務(wù)。

廣義線性模型：主要講述一些用于回歸的方法，其中目標(biāo)值y是輸入變量x的線性組合。數(shù)據(jù)概念表示為：如果y(w,x)=w0+w1x1+...+wpxp,在整個模塊中，我們定義向量w=(w1,...,wp)作為coef_，定義w0作為intercept_。

1.1.1.普通最小二乘法
LinearRegression擬合一個帶有系數(shù)w=(w1,...,wp)的線性模型，使得數(shù)據(jù)集實際觀測數(shù)據(jù)和預(yù)測數(shù)據(jù)（估計值）之間的殘差平方和最小。其數(shù)學(xué)表達式為:

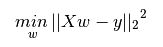
LinearRegression會調(diào)用fit方法來擬合數(shù)組 X,y,并且將線性模型的系數(shù)w存儲在其成員變量coef_中:

>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> reg.coef_
array([ 0.5,  0.5])

然而，對于普通最小二乘的系數(shù)估計問題，其依賴于模型各項的相互獨立性。當(dāng)各項是相關(guān)的，且設(shè)計矩陣X的各列近似線性相關(guān)，那么，設(shè)計矩陣會趨向于奇異矩陣，這種特性導(dǎo)致最小二乘估計對于隨機誤差非常敏感，可能產(chǎn)生很大的方差。例如，在沒有實驗設(shè)計的情況下收集到的數(shù)據(jù)，這種多重共線性（multicollinearity）的情況可能真的會出現(xiàn)。

線性回歸示例：

本示例僅使用糖尿病數(shù)據(jù)集的第一個特征，以說明此回歸技術(shù)的二維圖。 可以在圖中看到直線，該直線顯示了線性回歸如何嘗試?yán)L制一條直線，該直線將最大程度地減少數(shù)據(jù)集中觀察到的響應(yīng)與線性近似預(yù)測的響應(yīng)之間的殘差平方和。還計算輸出了系數(shù)，殘差平方和和方差得分。

import matplotlib.pyplot as pltimport numpy as npfrom sklearn import datasets, linear_modelfrom sklearn.metrics import mean_squared_error, r2_scoreimport pandas as pd#加載數(shù)據(jù)diabetes = datasets.load_diabetes()
# 取一個特征列維度diabetes_X = diabetes.data[:, np.newaxis, 2]#np.newaxis將矩陣轉(zhuǎn)換成一列# 劃分訓(xùn)練和測試數(shù)據(jù)集diabetes_X_train = diabetes_X[:-20]diabetes_X_test = diabetes_X[-20:]
# 劃分訓(xùn)練和測試目標(biāo)集diabetes_y_train = diabetes.target[:-20]diabetes_y_test = diabetes.target[-20:]
# 創(chuàng)建線性回歸模型regr = linear_model.LinearRegression()
# 使用數(shù)據(jù)集訓(xùn)練模型regr.fit(diabetes_X_train, diabetes_y_train)
# 使用測試集訓(xùn)練函數(shù)diabetes_y_pred = regr.predict(diabetes_X_test)
# 系數(shù)print('Coefficients: \n', regr.coef_)# 平均誤差print("Mean squared error: %.2f"% mean_squared_error(diabetes_y_test, diabetes_y_pred))# 變量預(yù)測分數(shù)print('Variance score: %.2f' % r2_score(diabetes_y_test, diabetes_y_pred))
# 可視化輸出plt.scatter(diabetes_X_test, diabetes_y_test,  color='black')plt.plot(diabetes_X_test, diabetes_y_pred, color='red', linewidth=3)
#橫縱坐標(biāo)plt.xticks(())plt.yticks(())
plt.show()

輸出：

Coefficients:
[938.23786125]
Mean squared error: 2548.07
Variance score: 0.47

關(guān)于“Sklearn廣義線性模型實例分析”這篇文章的內(nèi)容就介紹到這里，感謝各位的閱讀！相信大家對“Sklearn廣義線性模型實例分析”知識都有一定的了解，大家如果還想學(xué)習(xí)更多知識，歡迎關(guān)注創(chuàng)新互聯(lián)行業(yè)資訊頻道。

文章名稱：Sklearn廣義線性模型實例分析
標(biāo)題URL：http://www.chinadenli.net/article2/igpiic.html

成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián)，為您提供定制網(wǎng)站、關(guān)鍵詞優(yōu)化、網(wǎng)站設(shè)計、用戶體驗、品牌網(wǎng)站建設(shè)、移動網(wǎng)站建設(shè)

廣告

聲明：本網(wǎng)站發(fā)布的內(nèi)容（圖片、視頻和文字）以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主，如果涉及侵權(quán)請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網(wǎng)站立場，如需處理請聯(lián)系客服。電話：028-86922220；郵箱：631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載，或轉(zhuǎn)載時需注明來源： 創(chuàng)新互聯(lián)