圖的非連通遍歷
1、連通圖和非連通圖
珠山網(wǎng)站建設(shè)公司創(chuàng)新互聯(lián),珠山網(wǎng)站設(shè)計制作,有大型網(wǎng)站制作公司豐富經(jīng)驗。已為珠山上千家提供企業(yè)網(wǎng)站建設(shè)服務(wù)。企業(yè)網(wǎng)站搭建\成都外貿(mào)網(wǎng)站制作要多少錢,請找那個售后服務(wù)好的珠山做網(wǎng)站的公司定做!
連通圖:任意的一個頂點到任意的另外一個頂點都有著相應(yīng)的路徑所能夠到達(dá)。
非連通圖:只要找出了有一個頂點不能夠到達(dá)另外一個頂點。
2、遍歷
對于連通圖來說,通過DFS或BFS就可以完成遍歷;
對于非連通圖來說,就得從每個頂點出發(fā)進(jìn)行搜索,每一次的從一個新的頂點出發(fā)訪問,每個頂點都要開始搜索一遍。
3、非連通圖的遍歷算法
(1)、不可取的算法:沒有必要將非連通圖生成森林,在由森林生成我們的遍歷樹,然后再進(jìn)行樹形結(jié)構(gòu)的訪問。
(2)、比較好的算法:直接調(diào)動我們之前編寫好的DFS()函數(shù);只要沒有訪問的頂點,我們就由該頂點出發(fā)進(jìn)行深度優(yōu)先遍歷,這樣就最終把整個非連通圖就遍歷完成。
(3)強連通圖:針對有向圖,有A-->B的邊,一定也有B-->A的邊。
(4)、遍歷算法:
void components(){ //非連通圖的遍歷
int n = Graph<Type>::getCurVertex();
bool *visit = new bool[n];
for(int i = 0; i < n; i++){
visit[i] = false;
}
for(i = 0; i < n; i++){ //對每個頂點都看一下,是否訪問過。4
if(!visit[i]){
DFS(getValue(i), visit);
}
}
delete []visit;
}4、完整代碼、測試代碼、測試結(jié)果
(1)、完整代碼
#ifndef _GRAPH_H_
#define _GRAPH_H_
#include<iostream>
#include<queue>
using namespace std;
#define VERTEX_DEFAULT_SIZE 20
template<typename Type>
class Graph{
public:
bool isEmpty()const{
return curVertices == 0;
}
bool isFull()const{
if(curVertices >= maxVertices || curEdges >= curVertices*(curVertices-1)/2)
return true; //圖滿有2種情況:(1)、當(dāng)前頂點數(shù)超過了最大頂點數(shù),存放頂點的空間已滿
return false; //(2)、當(dāng)前頂點數(shù)并沒有滿,但是當(dāng)前頂點所能達(dá)到的邊數(shù)已滿
}
int getCurVertex()const{
return curVertices;
}
int getCurEdge()const{
return curEdges;
}
public:
virtual bool insertVertex(const Type &v) = 0; //插入頂點
virtual bool insertEdge(const Type &v1, const Type &v2) = 0; //插入邊
virtual bool removeVertex(const Type &v) = 0; //刪除頂點
virtual bool removeEdge(const Type &v1, const Type &v2) = 0; //刪除邊
virtual int getFirstNeighbor(const Type &v) = 0; //得到第一個相鄰頂點
virtual int getNextNeighbor(const Type &v, const Type &w) = 0; //得到下一個相鄰頂點
public:
virtual int getVertexIndex(const Type &v)const = 0; //得到頂點下標(biāo)
virtual void showGraph()const = 0; //顯示圖
virtual Type getValue(int index)const = 0;
public:
virtual void DFS(const Type &v) = 0; //深度優(yōu)先
virtual void BFS(const Type &v) = 0; //廣度優(yōu)先
protected:
int maxVertices; //最大頂點數(shù)
int curVertices; //當(dāng)前頂點數(shù)
int curEdges; //當(dāng)前邊數(shù)
};
template<typename Type>
class GraphMtx : public Graph<Type>{ //鄰接矩陣?yán)^承父類矩陣
#define maxVertices Graph<Type>::maxVertices //因為是模板,所以用父類的數(shù)據(jù)或方法都得加上作用域限定符
#define curVertices Graph<Type>::curVertices
#define curEdges Graph<Type>::curEdges
public:
GraphMtx(int vertexSize = VERTEX_DEFAULT_SIZE){ //初始化鄰接矩陣
maxVertices = vertexSize > VERTEX_DEFAULT_SIZE ? vertexSize : VERTEX_DEFAULT_SIZE;
vertexList = new Type[maxVertices]; //申請頂點空間
for(int i = 0; i < maxVertices; i++){ //都初始化為0
vertexList[i] = 0;
}
edge = new int*[maxVertices]; //申請邊的行
for(i = 0; i < maxVertices; i++){ //申請列空間
edge[i] = new int[maxVertices];
}
for(i = 0; i < maxVertices; i++){ //賦初值為0
for(int j = 0; j < maxVertices; j++){
edge[i][j] = 0;
}
}
curVertices = curEdges = 0; //當(dāng)前頂點和當(dāng)前邊數(shù)
}
GraphMtx(Type (*mt)[4], int sz){ //通過已有矩陣的初始化
int e = 0; //統(tǒng)計邊數(shù)
maxVertices = sz > VERTEX_DEFAULT_SIZE ? sz : VERTEX_DEFAULT_SIZE;
vertexList = new Type[maxVertices]; //申請頂點空間
for(int i = 0; i < maxVertices; i++){ //都初始化為0
vertexList[i] = 0;
}
edge = new int*[maxVertices]; //申請邊的行
for(i = 0; i < maxVertices; i++){ //申請列空間
edge[i] = new Type[maxVertices];
}
for(i = 0; i < maxVertices; i++){ //賦初值為矩陣當(dāng)中的值
for(int j = 0; j < maxVertices; j++){
edge[i][j] = mt[i][j];
if(edge[i][j] != 0){
e++; //統(tǒng)計列的邊數(shù)
}
}
}
curVertices = sz;
curEdges = e/2;
}
~GraphMtx(){}
public:
bool insertVertex(const Type &v){
if(curVertices >= maxVertices){
return false;
}
vertexList[curVertices++] = v;
return true;
}
bool insertEdge(const Type &v1, const Type &v2){
int maxEdges = curVertices*(curVertices-1)/2;
if(curEdges >= maxEdges){
return false;
}
int v = getVertexIndex(v1);
int w = getVertexIndex(v2);
if(v==-1 || w==-1){
cout<<"edge no exit"<<endl; //要插入的頂點不存在,無法插入
return false;
}
if(edge[v][w] != 0){ //當(dāng)前邊已經(jīng)存在,不能進(jìn)行插入
return false;
}
edge[v][w] = edge[w][v] = 1; //因為是無向圖,對稱的,存在邊賦為1;
return true;
} //刪除頂點的高效方法
bool removeVertex(const Type &v){
int i = getVertexIndex(v);
if(i == -1){
return false;
}
vertexList[i] = vertexList[curVertices-1];
int edgeCount = 0;
for(int k = 0; k < curVertices; k++){
if(edge[i][k] != 0){ //統(tǒng)計刪除那行的邊數(shù)
edgeCount++;
}
}
//刪除行
for(int j = 0; j < curVertices; j++){
edge[i][j] = edge[curVertices-1][j];
}
//刪除列
for(j = 0; j < curVertices; j++){
edge[j][i] = edge[j][curVertices-1];
}
curVertices--;
curEdges -= edgeCount;
return true;
}
/* //刪除頂點用的是數(shù)組一個一個移動的方法,效率太低。
bool removeVertex(const Type &v){
int i = getVertexIndex(v);
if(i == -1){
return false;
}
for(int k = i; k < curVertices-1; ++k){
vertexList[k] = vertexList[k+1];
}
int edgeCount = 0;
for(int j = 0; j < curVertices; ++j){
if(edge[i][j] != 0)
edgeCount++;
}
for(int k = i; k < curVertices-1; ++k)
{
for(int j = 0; j < curVertices; ++j)
{
edge[k][j] = edge[k+1][j];
}
}
for(int k = i; k < curVertices-1; ++k)
{
for(int j = 0; j < curVertices; ++j)
{
edge[j][k] = edge[j][k+1];
}
}
curVertices--;
curEdges -= edgeCount;
return true;
}
*/
bool removeEdge(const Type &v1, const Type &v2){
int v = getVertexIndex(v1);
int w = getVertexIndex(v2);
if(v==-1 || w==-1){ //判斷要刪除的邊是否在當(dāng)前頂點內(nèi)
return false; //頂點不存在
}
if(edge[v][w] == 0){ //這個邊根本不存在,沒有必要刪
return false;
}
edge[v][w] = edge[w][v] = 0; //刪除這個邊賦值為0,代表不存在;
curEdges--;
return true;
}
int getFirstNeighbor(const Type &v){
int i = getVertexIndex(v);
if(i == -1){
return -1;
}
for(int col = 0; col < curVertices; col++){
if(edge[i][col] != 0){
return col;
}
}
return -1;
}
int getNextNeighbor(const Type &v, const Type &w){
int i = getVertexIndex(v);
int j = getVertexIndex(w);
if(i==-1 || j==-1){
return -1;
}
for(int col = j+1; col < curVertices; col++){
if(edge[i][col] != 0){
return col;
}
}
return -1;
}
public:
void showGraph()const{
if(curVertices == 0){
cout<<"Nul Graph"<<endl;
return;
}
for(int i = 0; i < curVertices; i++){
cout<<vertexList[i]<<" ";
}
cout<<endl;
for(i = 0; i < curVertices; i++){
for(int j = 0; j < curVertices; j++){
cout<<edge[i][j]<<" ";
}
cout<<vertexList[i]<<endl;
}
}
int getVertexIndex(const Type &v)const{
for(int i = 0; i < curVertices; i++){
if(vertexList[i] == v){
return i;
}
}
return -1;
}
public:
Type getValue(int index)const{
return vertexList[index];
}
void DFS(const Type &v){
int n = Graph<Type>::getCurVertex();
bool *visit = new bool[n];
for(int i = 0; i < n; i++){
visit[i] = false;
}
DFS(v, visit);
delete []visit;
}
void BFS(const Type &v){
int n = Graph<Type>::getCurVertex();
bool *visit = new bool[n];
for(int i = 0; i < n; i++){
visit[i] = false;
}
cout<<v<<"-->";
int index = getVertexIndex(v);
visit[index] = true;
queue<int> q; //隊列中存放的是頂點下標(biāo);
q.push(index);
int w;
while(!q.empty()){
index = q.front();
q.pop();
w = getFirstNeighbor(getValue(index));
while(w != -1){
if(!visit[w]){
cout<<getValue(w)<<"-->";
visit[w] = true;
q.push(w);
}
w = getNextNeighbor(getValue(index), getValue(w));
}
}
delete []visit;
}
void components(){ //非連通圖的遍歷
int n = Graph<Type>::getCurVertex();
bool *visit = new bool[n];
for(int i = 0; i < n; i++){
visit[i] = false;
}
for(i = 0; i < n; i++){
if(!visit[i]){
DFS(getValue(i), visit);
}
}
delete []visit;
}
protected:
void DFS(const Type &v, bool *visit){
cout<<v<<"-->";
int index = getVertexIndex(v);
visit[index] = true;
int w = getFirstNeighbor(v);
while(w != -1){
if(!visit[w]){
DFS(getValue(w), visit);
}
w = getNextNeighbor(v, getValue(w));
}
}
private:
Type *vertexList; //存放頂點的數(shù)組
int **edge; //存放邊關(guān)系的矩陣
};
#endif(2)、測試代碼
#include"Graph3.h"
int main(void){
GraphMtx<char> gm;
gm.insertVertex('A');
gm.insertVertex('B');
gm.insertVertex('C'); //B的第一個鄰接頂點是C,
gm.insertVertex('D');
gm.insertVertex('E');
gm.insertVertex('F');
gm.insertVertex('G');
gm.insertVertex('H');
gm.insertVertex('I');
gm.insertVertex('J');
gm.insertVertex('K');
gm.insertVertex('L');
gm.insertVertex('M');
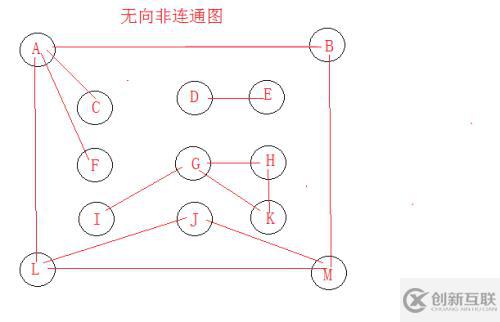
gm.insertEdge('A','B');
gm.insertEdge('A','C');
gm.insertEdge('A','F');
gm.insertEdge('A','L');
gm.insertEdge('B','M');
gm.insertEdge('L','J');
gm.insertEdge('L','M');
gm.insertEdge('J','M');
gm.insertEdge('D','E');
gm.insertEdge('G','H');
gm.insertEdge('G','I');
gm.insertEdge('G','K');
gm.insertEdge('H','K');
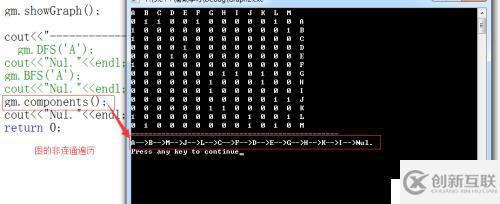
gm.showGraph();
cout<<"------------------------------------------------"<<endl;
gm.DFS('A');
cout<<"Nul."<<endl;
gm.BFS('A');
cout<<"Nul."<<endl;
gm.components();
cout<<"Nul."<<endl;
return 0;
}(3)、測試結(jié)果
測試圖的模型:
分享題目:圖的非連通遍歷
網(wǎng)站地址:http://www.chinadenli.net/article48/gpdeep.html
成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián),為您提供網(wǎng)站維護、云服務(wù)器、移動網(wǎng)站建設(shè)、企業(yè)網(wǎng)站制作、網(wǎng)站排名、網(wǎng)站設(shè)計公司
聲明:本網(wǎng)站發(fā)布的內(nèi)容(圖片、視頻和文字)以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主,如果涉及侵權(quán)請盡快告知,我們將會在第一時間刪除。文章觀點不代表本網(wǎng)站立場,如需處理請聯(lián)系客服。電話:028-86922220;郵箱:631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載,或轉(zhuǎn)載時需注明來源: 創(chuàng)新互聯(lián)

- 莆田企業(yè)建站:優(yōu)質(zhì)的企業(yè)網(wǎng)站應(yīng)該這樣做! 2021-10-19
- 你真的懂網(wǎng)站建造么?企業(yè)建站必定要了解這幾點 2016-12-01
- 企業(yè)建站有哪些要特別注意的點呢? 2016-11-27
- 網(wǎng)站建設(shè)企業(yè)建站過程當(dāng)中一定要注意的問題 2017-02-02
- 中小企業(yè)建站時怎么去規(guī)劃? 2023-02-21
- 中小企業(yè)建站應(yīng)該找什么樣公司 2014-10-31
- 廈門企業(yè)建站:建設(shè)網(wǎng)站如何做才能提高質(zhì)量? 2021-09-13
- 企業(yè)建站有哪些需要遵循的網(wǎng)站設(shè)計規(guī)則呢? 2016-08-30
- 企業(yè)建站怎么利用視頻元素 2016-10-24
- 企業(yè)建站前要了解哪些知識? 2016-09-26
- 企業(yè)建站該如何選擇心儀的建站公司 2015-04-11
- 為什么自適應(yīng)網(wǎng)站建設(shè)已成企業(yè)建站主流 2022-05-23